树
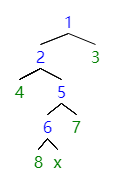
在线绘图 [1 [2 [4] [5 [6 [8][x]] [7] ] ] [3 ] x 不存在 只是代表8 是左节点
// 大概这样结构interface Node { val: number; children: Node[];}
const tree = { value: 1, children: [ { value: 2, children: [ { value: 4, children: [] }, { value: 5, children: [ { value: 6, children: [{ value: 8, children: [] }] }, { value: 7, children: [] }, ], }, ], }, { value: 3, children: [] }, ],};给定一个父节点,使用DFS遍历返回所有节点
深度优先搜索 DFS#
递归
const dfs = (node, res = []) => { res.push(node.value); // 遍历节点的每个孩子节点,并且在孩子节点上使用dfs递归 继续遍历 node.children.forEach((child) => dfs(child, res)); return res;};dfs(tree) // [ 1, 2, 4, 5, 6, 8, 7, 3 ]非递归
const dfs = (root) => { const stack = [root]; const res = []; while (stack.length) { const node = stack.pop(); res.push(node.value); let len = node.children && node.children.length; for (let i = len - 1; i >= 0; i--) { stack.push(node.children[i]); } } return res;};广度优先搜索 BFS#
const bfs = (root) => { if (!root) throw new Error(''); // 1、新建一个队列,把根节点入队 const queue = [root]; const res = []; // 4、重复第2,3步,直到队列为空 while (queue.length > 0) { // 2、把队头出队,并访问 const head = queue.shift(); res.push(head.value); // 3、把队头的children挨个入队 head.children.forEach((child) => { queue.push(child); }); } return res;};
bfs(tree) // [ 1, 2, 3, 4, 5, 6, 7, 8 ]二叉树#
二叉树的定义
// Definition for a binary tree node.function TreeNode(val, left, right) { this.val = val === undefined ? 0 : val; this.left = left === undefined ? null : left; this.right = right === undefined ? null : right;}递归前中后#
const preorderTraversal = (root) => { let res = []; if (!root) return res; const order = (node) => { // 主要就是这三个的顺序 res.push(node.val); // node.left && order(node.left) if (node.left !== null) order(node.left); if (node.right !== null) order(node.right); }; order(root); return res;};
const inorderTraversal = (root) => { };
const postorderTraversal = (root) => { };迭代#
迭代:显式维护一个栈
前序遍历#
- 前序
1 2 4 5 6 8 7 3
const preorderTraversal = (root) => { let res = []; if (!root) return res; let stack = []; stack.push(root); while (stack.length > 0) { let current = stack.pop(); res.push(current.val); if (current.right !== null) stack.push(current.right); if (current.left !== null) stack.push(current.left); } return res;};中序遍历#
- 中序
4 2 8 6 5 7 1 3
const inorderTraversal = (root) => { let res = []; if (!root) return res;
let stack = []; let temp = root; while (temp !== null) { stack.push(temp); temp = temp.left; } while (stack.length > 0) { let current = stack.pop(); res.push(current.val); if (current.right !== null) { let temp2 = current.right; while (temp2 !== null) { stack.push(temp2); temp2 = temp2.left; } } } return res;};const inorderTraversal = function (root) { const res = [], stack = []; while (root || stack.length) { // 中序遍历,首先迭代左孩子,左孩子依次入栈 if (root.left) { stack.push(root); root = root.left; // 如果左孩子为空了,输出节点,去右孩子中迭代, } else if (root.right) { res.push(root.val); root = root.right; // 如果左右孩子都为空了,输出当前节点,栈顶元素出栈,也就是回退到上一层,此时置空节点左孩子,防止while循环重复进入 } else if (!root.left && !root.right) { res.push(root.val); root = stack.pop(); root && (root.left = null); } } return res;};后序遍历#
- 后序
4 8 6 7 5 2 3 1
// 1, 先依次遍历左孩子, 在栈中依次记录,当左孩子为空时,遍历到叶子节点 //跳回上一层节点, 为防止while循环重复进入,将上一层左孩子置为空// 2, 接着遍历右孩子, 在栈中依次记录值,当右孩子为空时, 遍历到叶子节点// 跳回上一层节点, 为防止while循环重复进入,将上一层右孩子置为空
const postorderTraversal = (root) => { const res = []; const stack = []; while (root || stack.length) { if (root.left) { stack.push(root); root = root.left; } else if (root.right) { stack.push(root); root = root.right; } else { res.push(root.val); root = stack.pop(); if (root && root.left) root.left = null; else if (root && root.right) root.right = null; } } return res;};前序遍历的逆序思维
// 结果数组中依次进入的是节点的左孩子,右孩子,节点本身,注意使用的是// unshift,与前序遍历push不同,每次数组头部添加元素,实际上就是前序遍历的逆序过程const postorderTraversal = function(root) { const res = [], stack = [] while (root || stack.length) { res.unshift(root.val) root.left && stack.push(root.left) root.right && stack.push(root.right) root = stack.pop() } return res};BFS#
层序遍历#
const levelOrder = (root) => { const res = []; if (root === null) return res; const queue = []; queue.push(root); while (queue.length > 0) { const current = queue.shift(); res.push(current.val); if (current.left) queue.push(current.left); if (current.right) queue.push(current.right); } return res;};最短路径#
层序遍历 102
队列
判断当前元素有没有左右节点 有的话推出自己同时将左右节点加入新的队列
const queue = []queue.push(root)while(queue.length > 0){ let layerGroup = [] let len = queue.length for(let i = 0;i<len;i++){ let target = queue.shift() layerGroup.push(target) if(target.left) queue.push(target.left) if(target.right) queue.push(target.right) } res.push(layerGroup)}return res层次遍历 107
res.unshift(layerGroup)二叉树的右视图 199
相当于层序遍历后 取每一个数组的最后一个元素
二叉树的最近公共祖先 | LCA DFS 236
// 最近公共祖先 => LCAvar lowestCommonAncestor = function (root, p, q) { if (root === null || root === p || root === q) return root // 问题 缩小 递归遍历 左右 let left = lowestCommonAncestor(root.left, p, q) let right = lowestCommonAncestor(root.right, p, q) // 如果 left right 都有值 证明根节点就是它们的 LCA if (left && right) return root // 如果只有一边有值 就递归缩小 再次调用 return left ? left : right}
144 qian
94 zhong
//145 hou
一些练习#
二叉树反转#
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
3 / \ 9 20 / \ 15 7104. 二叉树的最大深度#
- DFS
- 终止条件:当前节点为空
- 返回值
- 节点为空时说明高度为 0,所以返回 0
- 节点不为空时则分别求左右子树的高度的最大值,同时加1表示当前节点的高度,返回该数值
var maxDepth = function(root) { if (!root) return 0; let left = maxDepth(root.left); let right = maxDepth(root.right); return Math.max(left, right) + 1;};111. 二叉树的最小深度#
- DFS
- 当前节点 root 为空时,说明此处树的高度为 0,0 也是最小值
- 当前节点 root 的左子树和右子树都为空时,说明此处树的高度为 1,1 也是最小值
- 如果为其他情况,则说明当前节点有值,且需要分别计算其左右子树的最小深度,返回最小深度 +1,+1 表示当前节点存在有 1 个深度
var minDepth = function(root) { if(root == null) { return 0; } if(root.left == null && root.right == null) { return 1; } let ans = Number.MAX_SAFE_INTEGER; if(root.left != null) { ans = Math.min(minDepth(root.left), ans); } if(root.right != null) { ans = Math.min(minDepth(root.right), ans); } return ans + 1;};112. 路径总和#
判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和
targetSum
- DFS
var hasPathSum = function (root, targetSum) { // 遍历到null节点 if (!root) return false; // 遍历到叶子节点 if (!root.left && !root.right) { return root.val === targetSum; } // 当前递归问题 拆解成 两个子树的问题,其中一个true了就行 return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val);};- BFS
- 进行广度优先遍历,使用两个队列,一个队列用于保存节点,一个队列用于保存对应节点到根节点的路径和。如果当前节点是叶子节点,则判断路径和是否等于sum。(使用栈也一样,只不过顺序不同而已,队列先遍历左子树,栈先遍历右子树)
var hasPathSum = function(root, targetSum) { if(root === null) return false; var queue1 = [root]; var queue2 = [root.val]; while(queue1.length !== 0){ var node = queue1.shift(); var rootVal = queue2.shift(); if(node.left == null && node.right == null && rootVal == targetSum){ return true; } if(node.left){ queue1.push(node.left); queue2.push(node.left.val + rootVal); } if(node.right){ queue1.push(node.right); queue2.push(node.right.val + rootVal); } } return false;};07. 重建二叉树#
输入某二叉树的前序遍历和中序遍历的结果,请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
function TreeNode(val) { this.val = val; this.left = this.right = null;}var buildTree = function (preorder, inorder) { if (!preorder.length || !inorder.length) return null;
let rootVal = preorder[0]; let rootIndex = inorder.indexOf(rootVal); const node = new TreeNode(rootVal);
node.left = buildTree( preorder.slice(1, rootIndex + 1), inorder.slice(0, rootIndex) ); node.right = buildTree( preorder.slice(rootIndex + 1), inorder.slice(rootIndex + 1) ); return node;};27. 二叉树的镜像#
递归
/** * function TreeNode(val) { * this.val = val; * this.left = this.right = null; * } */
var mirrorTree = function (root) { if (!root) return null; // 交换当前左右节点 let temp = root.left; root.left = root.right; root.right = temp; // 递归操作左右子树 mirrorTree(root.left); mirrorTree(root.right); return root;};辅助栈
- 特例化:针对
root为null的情况,直接返回root - 初始化:定义一个辅助栈,将根节点入栈
- 递归:判断栈不为空,则逐步出栈,将节点的左右节点互换,实现镜像
var mirrorTree = function (root) { if (root) { let stack = []; stack.push(root); while (stack.length > 0) { let node = stack.pop(); let temp = node.left; node.left = node.right; node.right = temp; if (node.left) stack.push(node.left); if (node.right) stack.push(node.right); } } return root;};树形数据扁平化#
const data = [ { id: 1, pid: 0 }, { id: 2, pid: 1 }, { id: 3, pid: 1 }, { id: 4, pid: 3 }, { id: 5, pid: 0 }, { id: 6, pid: 5 },];
[ { id: 1, pid: 0, children: [ { id: 2, pid: 1 }, { id: 3, pid: 1, children: [{ id: 4, pid: 3 }] }, ], }, { id: 5, pid: 0, children: [{ id: 6, pid: 5 }] },];递归#
// 先筛选出顶级数据 然后处理顶级和子集 最后递归处理子集与子集的子集function formatDataTree(data) { let parents = data.filter((p) => p.pid === 0); let children = data.filter((p) => p.pid !== 0);
dataToTree(parents, children);
return parents; // parents children 都是数组 function dataToTree(parents, children) { parents.map((p) => { children.map((c, i) => { if (c.pid === p.id) { // 优化点 let _children = JSON.parse(JSON.stringify(children)); _children.splice(i, 1); dataToTree([c], _children); if (p.children) { p.children.push(c); } else { p.children = [c]; } } }); }); }}扁平化数据#
filter#
function formatDataTree2(data) { let _data = JSON.parse(JSON.stringify(data)); return _data.filter((p) => { let _arr = _data.filter((c) => c.pid === p.id); _arr.length && (p.children = _arr); return p.pid === 0; });}reduce#
const formatDataTree3 = (data) => { return data.reduce((total, item, index, list) => { if (item.pid === 0) { total.push({ ...item, children: list.filter((c) => c.pid === item.id) }); } else { item.children = list.filter((c) => c.pid === item.id); } return total; }, []);};其他案例#
ref
- 第一个回答很赞 一道JS树状对象遍历算法题,求解?
递归下去,回溯上来,这就是DFS的简单逻辑。而BFS则是层层递进的逻辑。
var nodes = { value: 1, children: [ { value: 2, children: [ { value: 4, children: [{ value: 6 }], }, { value: 3, children: [{ value: 7 }], }, // ... ], }, { value: 5, children: [{ value: 8 }], }, // ... ],};DFS
const dfs = ({ value = 0, children = [] }) => { return children.reduce((result, node) => result + dfs(node), value);};console.log(dfs(nodes));BFS
const bfs = (nodes, result = 0) => { const stack = [nodes]; while (stack.length) { const { value = 0, children } = stack.pop(); result += value; if (children) stack.push(...children); } return result;};JSON 序列化
JSON.stringify(nodes) .replace(/\D+/g, '-') .split('-') .reduce((a, b) => Number(a) + Number(b), 0)